شرودنجر الجميلة .. كيف بنيت وإلى ماذا توصلت ؟

بعد اكتشاف ماكس بلانك لكمومية الضوء وتفسير أينشتاين بأن تسمية "الكم " quanta الذي استخدمها بلانك هو عبارة عن فوتون أو "جسيم ضوئي" ، واقترح اعتبار أن تكون طاقة الفوتون متناسبة مع تردده ، فكانت تلك الفكرة من أول الافتراضات الخاصة بازدواجية الموجة والجسيم.
ونظرا لكون الطاقة وكمية الحركة الحركة ينتسبان إلى التردد والعدد الموجي في النظرية النسبية الخاصة ، فينتج عن ذلك أن كمية الحركة للفوتون يكون متناسبا طرديا مع عدده الموجي .

وافترض لويس دي برولي أن هذا ينطبق على جميع الجسيمات ، بما فيها الإلكترون. وبين انه بافتراض أن الموجة المادية تتقدم مزاملة لجسيمها ، فإن الإلكترون يكوّن موجة راكدة ، بمعنى أنه يحتوي على ترددات زاوية منفصلة فقط حول النواة الذرية وهي التي تكون مسموحة له باتخاذها
تلك المدارات الكمومية في الذرة تنتمي إلى مستويات طاقة منفصلة (أي لها قيم خاصة ذاتية)، واستطاع دي برولي تفسير نموذج بور للبنية الذرية وما تحويه من مستويات للطاقة. وكان نموذج بور معتمدا على التصور الكمومي للعزم الزاوي (أي تكون له قيم خاصة ذاتية) :

وطبقا ل "دي برولي " يوصف الإلكترون بموجة ذات عدد صحيح من طول الموجة ، وأنه في الذرة لا بد وأن يناسب العدد الموجي محيط مدار الإلكترون:

ولكن هذا الافتراض يحصر موجة الإلكترون في بُعد واحد ويدور في مدار دائري.
وابتداء من تلك الافتراضات علّق الفيزيائي بيتر ديباي بأنه إذا كان الجسيمات تتصرف بخصائص الموجات فلا بد لها أن تفي بنوع من أنواع دالة موجية. ومن ذلك التعليق الذي قدمه "ديباي" حاول شرودنجر التوصل إلى معادلة موجية في ثلاثة أبعاد تنطبق على الإلكترون. واستعان بما قام به هاميلتون من بيان التناظر بين ميكانيكا الأجسام وخواص الضوء والذي يتمثل في المشاهدة أن الحد الصفري لطول الموجة (أي عندما يصل طول الموجة إلى 0) يعادل حالة نظام في الميكانيكا الكلاسيكية. وتوصل شرودنجر إلى المعادلة :

تسمح لنا معادلة شرودنجر لحساب الدوال الموجية لنظام وكيف تتغير مع الزمن. ولكن معادلة شرودنجر لا تقول "ما هي " الدالة الموجية بالضبط. وتعتني تفسيرات ميكانيكا الكم بأسئلة مثل العلاقة بين الدالة الموجية والحقيقة الواقعية ونتائج قياسات التجارب.وبينما تحسب الميكانيكا التقليدية مسار 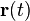جسيم بدقة يظهر مكان الجسيم في ميكانيكا الكم كقيمة محتملة لدوال توزيع ، تعطيها معادلة شرودنجر.

ويوصف الجسيم كحزمة موجية فإذا كان اتساع الحزمة الموجية قصيرا جدا فيمكن تحويل معادلة شرودنجر إلى معادلة نيوتن اللحركة. . 

تصاغ الدوال الموجية في معادلة شرودنجر في صورة معاملات طبقا لتصور شرودنجر. وفي تصور هايزنبرج الذي حل مسألة طيف الهيدروجين بميكانيكا الكم فقد صاغ معادلات الحركة مباشرة بدلا من المعاملات. وتسمى طريقة هايزنبرج التي استخدم فيها حساب المصفوفات وتسمى "معادلات هايزنبرج للحركة". 

وكلا الطريقتين : معادلة شرودنجر أو

معادلات الحركة لهايزنبرج

متماثلتان من وجهة النتائج.
وقد توصل هايزنبرج لطريقته عام 1923 أي قبل توصل شرودنجر لمعادلته التي صاغها عام 1926.

رفض أينشتاين ميكانيكا الكم باعتبارها لا تصف مكان جسيم بدقة مثلما في الميكانيكا الكلاسيكية وتعطي فقط احتمال وجود الجسيم في مكان معين .
ولكن التوافق بين طريقة هايزنبرج الكمومية ومعادلة شرودنجر والنجاح التي حازته ميكانيكا الكم في تفسير ظواهر طبيعية كثيرة تعجز الميكانيكا الكلاسيكية عن حسابها وتفسيرها ثبتت من مزكز ميكانيكا الكم كطريقة يمكن الاعتماد عليها في تفسير الظواهر الطبيعية على المستوى الصغري في عالم الذرات والجزيئات والجسيمات الأولية.

 الخلاصة : كل جسيم يمكن التعبير عنه بواسطة الدالة الموحية ابساي وهي دالة في الموضوع والزمن ومربعها يعبر عن احتمالية ايجاد الجسيم في مكان محدد عند زمن معين.

كثافة احتمال وجود الإلكترون في المدارات الأولى لذرة الهيدروجين مبينة كمقاطع مستوية أحجام المدارات ممثلة هنا بمقاييس رسم مختلفة.

المصدر : ويكيبيديا و ادخل هنا ... بتصرف

#syrianphysics #فيزياء_من_سورية